Fractals

Introduction

Fractals were one of the most fascinating thing to me when I was in primary school, and today I hope to share some of that fascination with you.

What are fractals? The definition is debated among mathematicians, but one of the defining features is being self-similar: a small part of image is similar to the whole thing.

There are a lot of examples of self-similar structures in nature. A snowflake under a microscope has the basic hexagonal shape, but on each of the six branches, when you zoom in, you see smaller crystals.

Snowflakes are just water crystals, other crystals in chemistry also display this feature and are strikingly beautiful. Othe examples include veins of leaves, our own blood circulatory system, and this weird broccoli thing:

Fractals are things that when you zoom in to a smaller part of itself, you get something that resembles the original. This definition will make a lot more sense once we see mathematical examples.

The Sierpiński Triangle

Arguably one of the most iconic fractal, I loved it during childhood and so did many other mathematicians. I have a friend who still signs all the cards with a drawing of the Sierpiński Triangle. Outside the Cambridge maths department, there is a model of the 3D version of this.

The Sierpiński Triangle is very easy to construct. Start from one equilateral triangle. Then, find the midpoint of each of the sides. Connect the three dots, and you get a inverted copy of an equilateral triangle in the middle. This part we remove from the original shape, which re represent here by erasing the black color.

After this, we are left with 3 smaller equilateral triangles inside of the bigger one. For each of these 3 smaller triangles, we repeat the previous step.

Once we do this, we are left with 9 triangles which are even smaller. For each of those triangles, we repeat the same step.

Now suppose that we let this process go on infinitely many times. The resulting image is the Sierpiński Triangle. We can get a sense of what the picture looks like by repeating the process 4 or 5 times.

Take the final Sierpiński Triangle. If we look at one of the three smaller triangular shapes that make up the original picture, then this is just a copy of the original, but shrunk to 1/4 of its original size. And no matter how much you zoom in, no matter which small triangular shape you take, they are always a smaller copy of the original.

This shape is particular in many aspects. For instance, what is the area of this image? Suppose that we started with a triangle of area 1. Then after the first step, we have divided the original triangle into 4 equal parts and deleted one of these parts. So we are left with 3/4 of the area.

Each of the 3 smaller triangles that are left become a copy of the original, so in the next step, the area of each small triangle is reduced to 3/4 of the small triangle. The total area left is now 3/4 × 3/4.

The area of the images we draw down goes from 1 to 3/4 to 3/4 × 3/4 to 3/4 × 3/4 × 3/4…

So the total area of the Sierpiński triangle is zero! But if you look at the total length of edges we have drawn to construct it, the “perimeter” if you will, is in fact infinite. We mentioned snowflakes earlier, a similar construction is the Koch Snowflake.

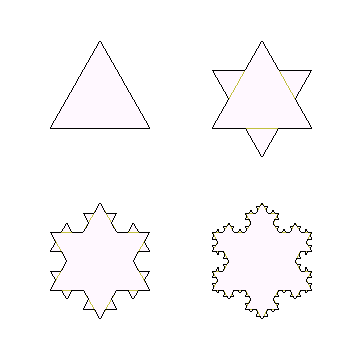
Try it yourself to draw it! Using programming tools to simulate the Sierpiński triangle and the Koch snowflake on your own is also very fun.

Fractal Dimensions

If you look at the Sierpiński Triangle, I wonder if you could tell me, how many dimensions does it have. An example of a two dimensions object is a square. But the Sierpiński Triangle doesn’t look like a square — it has area 0, so it can’t be 2 dimensions, can it? Something with dimension 1 is something like a line, but the Sierpin ́ski Triangle has too many squiggles, it would be very difficult to fold it up using a line.

The Sierpiński Triangle lives in the space between two dimensions, and mathematicians characterized it by giving it a fractal dimension, which is around 1.585. A lot of the fractals live in a strange in between space between dimensions, thus having non-integer dimensions.

I cannot talk about fractals without mentioning one of the most studied fractals of mathematics, which is the Mandelbrot set.

The self-similar property is very evident here, but more interestingly, the boundary of the Mandelbrot set is so squiggly, that it has fractal dimension 2!

PDF