Prisoner's Dilemma
Introduction
Let’s imagine for a second that you and a stranger are being interrogated by the police. A heinous crime has been committed, and the police has irrefutable proof that at least one of you was the perpetrator.
Here’s the deal (regardless of whether or not you actually did it):
- If you both cooperate with the police and admit the crime, you both get 1 year in prison.
- If one of you cooperates and admits the crime, and the other defects and claims innocence, then the corporator gets 10 years in jail, while the other walks free.
- If both of you defects, and refuse to admit the crime, both of you gets 6 years in jail.

What will you do in this situation? Would you change your answer if the stranger is changed to your best friend? Your enemy? A close family member? How would your answer change if the penalties change to larger numbers? For example, what if instead of a -6 years penalty for both defecting, you get life sentences instead?
This classic mind experiment is called a Prisoner’s Dilemma. Though theoretical in construct, it is relevant in a lot of real life scenarios.
The most chilling example is perhaps nuclear arm race. In a situation where two countries posses nuclear weapons, but don’t know the other country’s intentions, a prisoner’s dilemma is formed. The best outcome, of course, is if neither of the countries fires. But what if your neighbor is greedy and is going to fire?
The Rational Solution
There is a rational solution to the prisoner’s dilemma, which I found quite depressing.
Let’s go back to the original problem given in Table 1. Suppose that you are the prisoner, let’s split this problem into two cases based on whether your opponent defects or not.
• Suppose your opponent defects, what should you do? Based on the table, it is better for you if you defect as well. • Suppose your opponent defects, what should you do? You also gain the maximum benefit by defecting.
So the stunning conclusion is that you should always defect, no matter what. But this is also sad and unsatisfying, because we would never get the net best outcome for both people, which happens when we both cooperate.
We should cooperate only when we are sure that the other person would coorperate back. But how can we know this?
The Dilemma Repeated
In one variation of the game, the prisoner is given the dilemma over and over again. In this scenario, we can gauge how trustworthy the person is based on their past behavior.
For example, you could start by cooperating, and only cooperate in the next round if your opponent cooperated back in the previous round. If your opponent defected, then you never cooperate with them again.
Or, say if you have inside information about how likely your opponent is cooperate, then based on exact punishments, you could choose to cooperate with a certain probability. Since the game is played many times, the occasional bad luck won’t matter.
I won’t get into more details here since this excellent TEDed video explains everything very well with wonderful felt stop motion.
The Dilemma Robots
In real life, we don’t have the luxury of replaying each decision infinitely many times to see what the outcomes could be. How then, can we model the prisoners and the decisions?
We can do this by replacing the prisoners with robots, i.e. computer programs, and let them face off against each other.
We said that we can only rationally cooperate if we know the opponent will cooperate back. This happens, for instance, if your opponent is someone who places your well-being above their own, like your parents. They will cooperate no matter what you might do, so you can safely cooperate back.
We can model this behaviour with CooperateBot. CooperateBot always cooperate, no matter what happens.
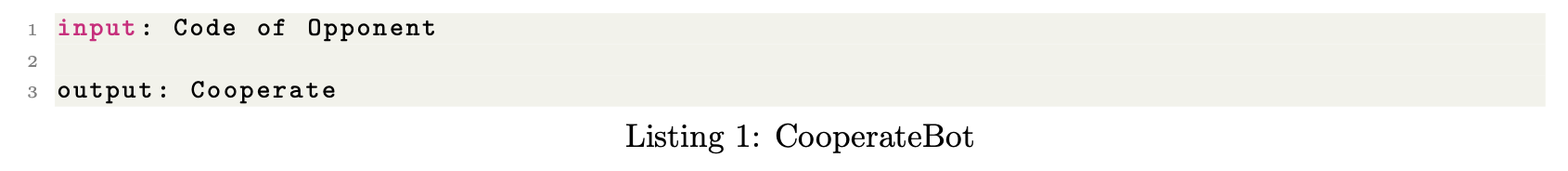
We can then design a robot which cooperates with CooperateBot only. We can call this CoopWith- CoopBot (I know this is a stupid name, if you have a better suggestion I’m listening):

We are assuming here that all of the computer programs are completely transparent, so one robot can see the inner working of any another robot, and the code of one robot can be the input of another robot, which is what we have done here.
What happens if you pitch CooperateBot against CooperateBot? With CoopWithCoopBot? What about pitching CoopWithCoopBot against CoopWithCoopBot?
The answer to the last question is they both defect. So we might improve upon CoopWithCoopBot, by introducing a MirrorBot:

What does this robot do? It looks at the opponent, and if the opponent is exactly the same as itself, i.e. a MirrorBot, then it cooperates. Otherwise it defects.
If we pitch MirrorBot against MirrorBot, both cooperate. But this system is fragile. Even if the Robot bahaves exactly MirrorBot, but the “spelling is different”, meaning the code deviates by even one letter, then this system fails.
We go back to the parents example. Your opponent doesn’t have to be CooperateBot for you to cooperate with them, you only need to know that they will Cooperate with you. So how about the following SmartBot:

SmartBot works like this: it works out how the opponent will react when pitched against SmartBot. That is: SmartBot takes the opponent code, and inputs itself into the code of the opponent. Then SmartBot observes the results. If the Opponent cooperates with SmartBot, then SmartBot cooperates back. Otherwise, SmartBot defects.
What happens if SmartBot is pitched against SmartBot? An infinite loop occurs. We can solve this problem by adding a timeout option in the robot: if a conclusion is not reached within, say, one hour, then output cooperate.
In this new scheme, SmartBot cooperates with SmartBot, and with CooperateBot.
I gave the ideas only, the actual implementation is a bit more tricky. For starters, to design MirrorBot and SmartBot, we need a program that knows its own source code.
This is possible but tricky: try it yourself! Try to design a robot that when it runs, outputs its own source code. Can you see an issue with this?
Origin Story
The idea behind the talk and the dilemma facing robots comes from Mihaly Barasz and his 2021 paper.
In 2019, I was 17 and was lucky to attend a summer camp called European Summer Program of Rationality (ESPR). The camp was fantastic and Mihaly was an instructor there. He gave a class on the prisoners dilemma, and it left an impression on me. So all credit of this talk goes to him.